11437 LCA (백준) 문제풀이

문제 

https://www.acmicpc.net/problem/11437

11437번: LCA

 

 

문제 접근 방식

트리 상에서 두 노드의 가장 가까운 조상 노드를 구하는 문제이며, 문제를 풀기 위해 아래 2가지를 집중적으로 고려했다.

1. 공통 조상 노드를 어떻게 구할 것인가?
2. 트리를 어떻게 표현할 것인가?

 

1. 공통 조상 노드를 어떻게 구할 것인가?

아래 그림처럼 구하고자 하는 두 개의 노드가 주어졌을 때, 공통 조상 노드를 찾기 위해 각자 거슬러 올라가보았다. 첫번째 노드가 조상으로 가기 위해서는 3번 올라가야하며, 두번째 노드는 2번 올라가야한다. 두 노드의 레벨이 다르기 때문에 이동하는 횟수가 다르다. 두 노드의 레벨이 같다면 둘 다 1씩 감소시키며 공통 조상 노드가 나올 때까지 반복하면 된다는 것 또한 알 수 있다. 

 

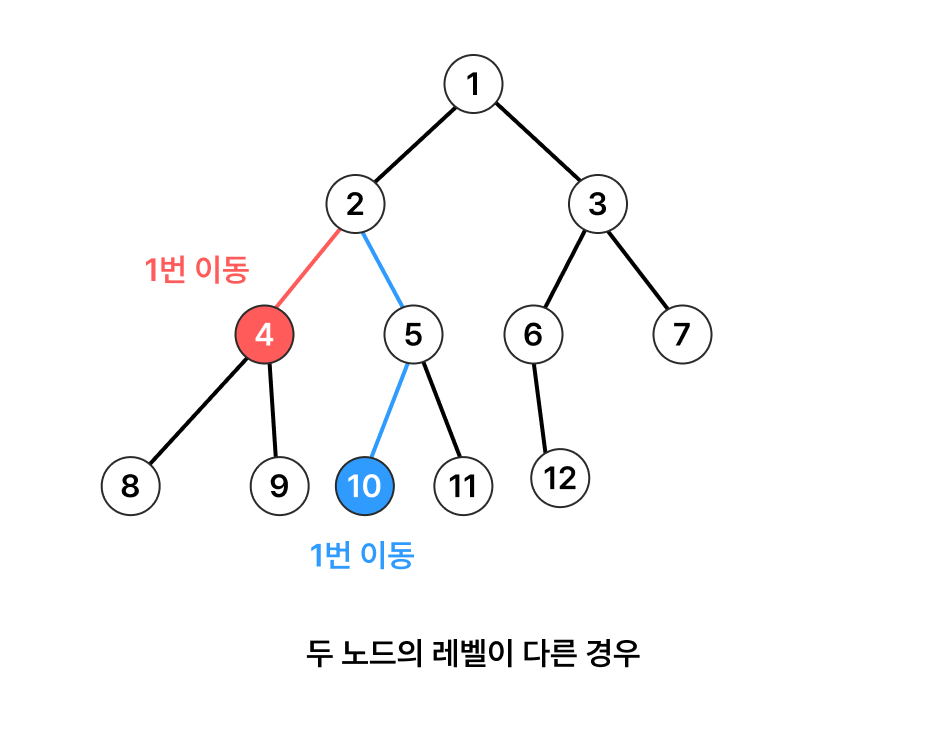
이 문제에서는 트리의 레벨이 중요한 역할을 하는 것을 알 수 있으며, 이를 위해 각 노드마다 레벨을 저장할 자료구조가 필요하다. 또한, 조상을 구하기 위해 트리를 거슬러 올라가야하기 때문에 부모노드를 저장하는 자료구조도 필요하다.

 

각 노드마다 부모 노드가 누구인지 깊이는 얼마인지를 구해놨다고 가정했을 때, 가장 가까운 공통 조상 노드를 구하는 방식은 아래와 같다.

1. 두 노드의 레벨을 구한다.
2. 두 노드의 레벨을 맞춘다 >> 상대적으로 깊은 노드를 깊이 차 만큼 이동시킨다.
3. 공통 조상 노드가 나올 때 까지 깊이를 하나씩 감소시킨다.

 

 

2. 트리를 어떻게 표현할 것인가?

각 노드의 부모 노드와 높이를 저장하기 위해서는 주어지는 N-1개의 노드 관계를 활용해야한다. 이를 위해 아래와 같은 방식으로 트리를 초기화 하였다.

1. 인접리스트에 각 노드마다 연결되는 노드를 추가한다.
2. 루트 노드인 1번을 시작으로 큐를 반복 순회한다. # 큐 : (자식,부모)쌍으로 저장됨
    2.1. 현재 노드의 부모노드와 높이를 설정한다.
    2.1. 자식 노드들을 순회하면서 (자식 노드, 현재 노드)를 큐에 넣어준다.

 

 

 

코드

import sys
input=sys.stdin.readline
print=sys.stdout.write
class LCA:
    # 두 노드의 연결 관게를 인접 리스트에 넣고, set_tree를 통해 트리를 초기화한다.
    def __init__(self,n):
        self.adj=[[] for _ in range(n+1)]
        for _ in range(n-1):
            u,v=map(int,input().split())
            self.adj[u].append(v)
            self.adj[v].append(u)

        self.set_tree()

    # 루트노드를 시작으로 아래로 내려가면서 parents 와 levels를 설정해준다.
    def set_tree(self):
        self.parents = [0] * (n + 1)
        self.levels = [0] * (n + 1)

        q=[(1,1)] # (자식노드, 부모노드)
        while q:
            now,parent=q.pop(0)

            self.parents[now]=parent
            self.levels[now]=self.levels[parent]+1

            for next in self.adj[now]:
                if next==parent: # 부모노드도 현재 노드와 연결되어 있기 때문에 부모노드는 Pass 해준다.
                    continue
                q.append((next,now))


    # u,v의 가까운 공통 조상을 구해준다.
    # 우선 u,v의 높이를 구해서 u와 v의 높이를 맞추고
    # 깊이를 하나씩 올려가면서 공통 조상이 나올때까지 반복한다.
    def get_common_ancestor(self,u,v):
        u_level=self.levels[u]
        v_level=self.levels[v]
        if u_level>v_level: # 깊이가 낮은 노드를 u 로 셋팅
            u,v=v,u
            u_level,v_level=v_level,u_level

        gap=v_level-u_level # 깊이 차이만큼 v를 루트쪽으로 이동시킨다.
        for _ in range(gap):
            v=self.parents[v]

        while u!=v: # 두 노드를 이동시키면서 공통 조상 노드가 나오는지 확인한다.
            u=self.parents[u]
            v=self.parents[v]

        return u # 공통 조상 노드를 반환한다.

if __name__=='__main__':
    n=int(input())
    lca=LCA(n)

    m=int(input())
    for _ in range(m):
        u,v=map(int,input().split())
        print(str(lca.get_common_ancestor(u,v))+'\n')

 

 

회고

처음 트리를 만들 때, Union Find 자료구조를 활용하면 되겠다 싶어서 아래와 같은 코드로 진행을 했는데 실패했다. 원인을 살펴보니 <그림> 과 같이 트리가 비연결 그래프 형식으로 연결이 되는 경우에는 처리가 되지 않는다. 이를 해결하기 위해 유니온 파인드가 아닌 단순 연결리스트를 통해 두 노드간 관계를 표시하도록 수정했다.

 

<그림>

 

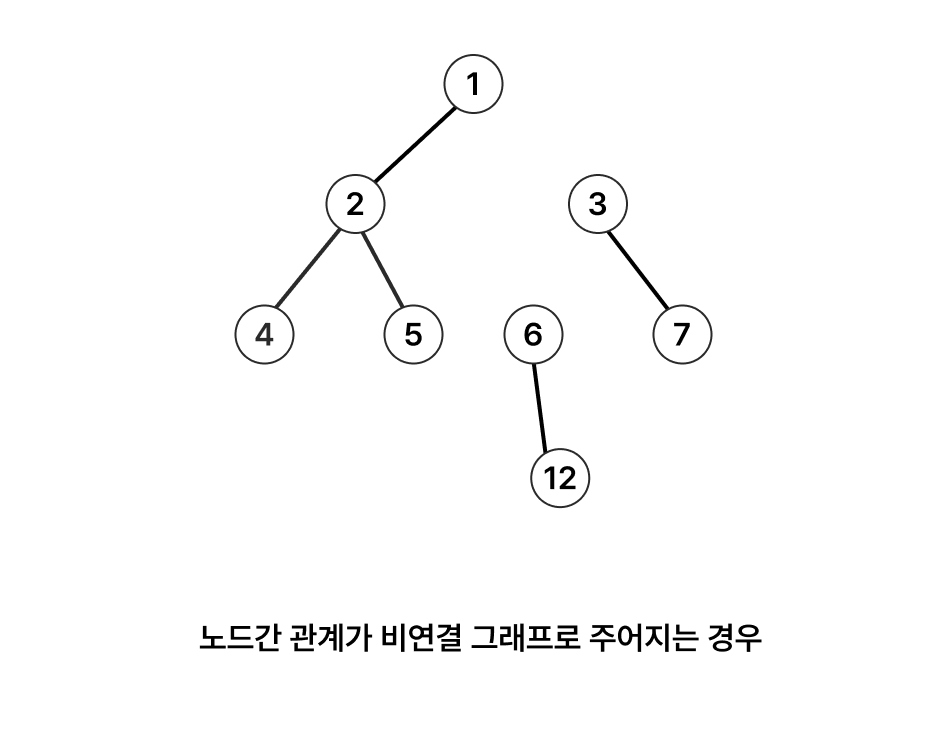
유니온 파인드로 구현한 실패 코드

import sys
input=sys.stdin.readline
print=sys.stdout.write
class UnionFind:
    def __init__(self,n):
        self.parents=[0]*(n+1)
        self.heights=[0]*(n+1)
        self.parents[1]=1
        self.heights[1]=1

    def find_parent(self,node):
        if self.parents[node]==node:
            return node
        return self.parents[node]

    def union(self,u,v):
        u_height=self.heights[u]
        v_height=self.heights[v]
        if u_height==0:
            u,v=v,u
            u_height,v_height=v_height,u_height

        self.parents[v]=u
        self.heights[v]=u_height+1

    def get_common_ancestor(self,u,v):
        u_h=self.heights[u]
        v_h=self.heights[v]
        if u_h>v_h:
            u,v=v,u
            u_h,v_h=v_h,u_h

        gap=v_h-u_h
        for _ in range(gap):
            v=self.parents[v]

        while u!=v:
            u=self.find_parent(u)
            v=self.find_parent(v)

        return u

if __name__=='__main__':
    n=int(input())
    union_find=UnionFind(n)

    for _ in range(n-1):
        u,v=map(int,input().split())
        union_find.union(u, v)

    m=int(input())
    for _ in range(m):
        u,v=map(int,input().split())
        print(str(union_find.get_common_ancestor(u,v))+'\n')