문제
https://school.programmers.co.kr/learn/courses/30/lessons/258705
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr

문제 접근 방식
10007로 나눠서 정답을 구하는 문제이다 보니 계속해서 값을 누적하는 DP 문제임을 야매로 알 수 있었지만,,어떤 점화식을 세울 수 있는지 감도 안와서 다른 분의 풀이를 참고했다. 특이한 접근과 점화식을 위한 메모제이션 변수를 2개 사용해야하는 문제라서 이해하는데 시간이 걸렸다.
점화식 정의
우선, 메모제이션을 위한 변수 a[ i ]와 b[ i ]를 두며 점화식의 정의는 아래와 같다(그림 참고)
a[i]= i번째 역삼각형을 기준으로 우측 하단 정삼각형을 마름모로 채울때의 경우의 수
b[i]= i번째 역삼각형을 기준으로 a[i]의 마름모가 아닌 방식으로 채우는 경우의 수
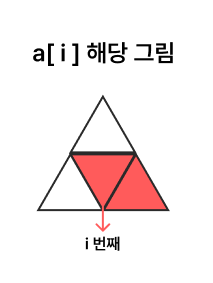
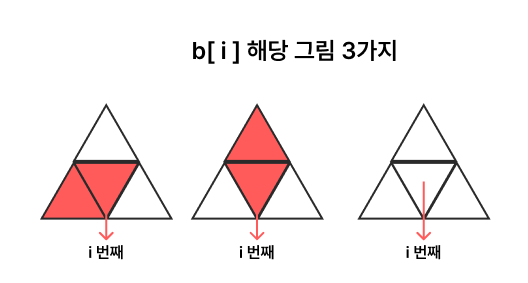
이렇게 정의를 해줌으로써 특정 구간별로 나눠서 생각할 수 있다.

점화식
a[i], b[i]의 점화식 정의를 토대로 점화식을 세우면 아래와 같다.
a[i]=a[i-1]+b[i-1]
b[i]의 경우 case가 나뉨
1. i번째 역삼각형 위에 정삼각형이 존재한다면
>> b[i]= a[i-1]*2 + b[i-1]*3
2. i 번째 역삼각형 위에 정삼각형 존재 x라면
>> b[i] = a[i-1]+b[i-1]*2
점화식 설명
b[ i ]의 점화식
a[ i ]를 설명하기에 앞서 b[ i ] 부터 설명을 하고 넘어가겠다.
i 번째 역삼각형 위에 정삼각형이 놓여져 있는지 여부에 따라 경우의 수가 달라진다.
1. 정삼각형이 위에 올려져 있는 경우
이때, 이전 i-1 번째에 대해 오른쪽 하단이 마름모로 채워져있는가( a[ i - 1]), 그렇지 않은가( b[ i - 1]) 로 나눠 생각할 수 있다.
a[ i - 1] 인경우에는 2가지의 경우가 존재하며, b[ i - 1] 인 경우에는 3가지의 경우가 존재한다
따라서, b[ i ] = a[ i - 1] x 2 + b[ i - 1 ]x3 이 된다.


2. 정삼각형이 위에 존재하지 않는 경우
이렇게 되는 경우, 그림과 깉이 a[ i - 1] 인 경우에는 1가지, b[ i -1 ] 인 경우는 2가지가 존재한다.
따라서 b[ i ] = a[ i - 1 ] + b[ i -1 ]x 2 이다.


a[ i ]의 점화식
a[ i ]의 경우는 정삼각형이 위에 존재하든 안하든 나올 수 있는 경우의 수는 a[ i - 1] 이 1개, b[ i - 1 ]이 1개 이다(그림에서는 존재하는 경우를 표현했으며, 위에 정삼각형을 지워도 경우의 수에는 변화가 없다)


시간 복잡도
DP를 활용하여 한번의 for문을 수행하며, 최댓값이 1e5이므로 시간내에 동작한다.
코드
def solution(n, tops):
MOD = 10007
a = [0] * (n + 1)
b = [0] * (n + 1)
a[0] = 0
b[0] = 1
tops.insert(0,0)
for i in range(1,n+1):
a[i]=(a[i-1]+b[i-1])%MOD
if tops[i]==1:
b[i]=(2*a[i-1]+3*b[i-1])%MOD
else:
b[i]=(a[i-1]+b[i-1]*2)%MOD
return (a[n]+b[n])%MOD
회고
메모제이션 변수를 2개 활용하는 방법과, 연속한 도형을 어떻게 쪼개서 생각하는지 경험할 수 있었다.
DP 문제임을 파악했다면 이전항과의 점화식을 세우려고 노력하자..
'문제풀이 > 프로그래머스' 카테고리의 다른 글
| 멀쩡한 사각형(프로그래머스) 문제풀이 (0) | 2024.03.28 |
|---|---|
| 방금 그곡(카카오) 문제풀이 (0) | 2024.03.28 |
| 숫자 블록(프로그래머스) 문제풀이 (0) | 2024.03.21 |
| 조이스틱(프로그래머스) 문제풀이 (0) | 2024.03.21 |
| 시소짝꿍(프로그래머스) 문제풀이 (0) | 2024.03.21 |