문제
https://www.acmicpc.net/problem/1865
1865번: 웜홀
첫 번째 줄에는 테스트케이스의 개수 TC(1 ≤ TC ≤ 5)가 주어진다. 그리고 두 번째 줄부터 TC개의 테스트케이스가 차례로 주어지는데 각 테스트케이스의 첫 번째 줄에는 지점의 수 N(1 ≤ N ≤ 500),
www.acmicpc.net

문제 접근 방식
도로를 통해 가중치 간선, 웜홀이라는 것을 통해 음의 가중치를 표현하였다. 또한, 도로는 무방향이라는 특징을 가진다.
이 문제의 목적은 출발 하였을 때보다 시간이 되돌아가는 경우의 여부를 구하는 문제로, 이는 그래프에서 음의사이클이 존재하는지를 판단하는 것과 동일하다.
아래의 이유로 벨만 포드 알고리즘을 활용해야한다는 것을 알 수 있다.
1. 가중치 그래프(음수 가능)
2. 음의 사이클 판별
짚고 넘어가야할 부분
1. 중복 간선과 웜홀을 어떻게 처리할 것인가?
2. 벨만 포드를 어떻게 사용할 수 있을까?
1. 중복 간선과 웜홀을 어떻게 처리할 것인가?
인접 행렬로 최솟값을 갖는 간선만 남긴 후, 이 간선들을 리스트로 변환
왜 이렇게 풀었나?
음의 사이클의 존재를 확인하기 위해서는, 웜홀을 포함하여 두 노드간 가장 작은 값을 갖는 간선만이 의미가 있고 그 이외의 도로는 불필요하다.
모든 간선을 인접 리스트에 다 넣어서 진행하기 보다는 최솟값을 가지는 간선만을 인접 리스트에 넣으면 될 것 같다는 생각이 들었다. 이를 위해서 인접 행렬을 사용하여 간선간 최솟값만을 저장했고, 이를 토대로 최소 길이 간선만을 리스트 edges에 넣어주었다.
# 인접행렬을 사용하여 최소 길이의 간선만 남길 예정
matrix=[[MAX for _ in range(n+1)] for _ in range(n+1)]
# 무방향 그래프이기 때문에, 각각의 방향을 쪼개며 최소 길이만을 저장
for _ in range(m):
s,e,t=map(int,input().split())
matrix[s][e]=min(matrix[s][e],t)
matrix[e][s]=min(matrix[e][s],t)
# 웜홀의 경우 단방향이며, 마이너스를 붙여서 음의 간선으로 만들어줌
for _ in range(w):
s,e,t=map(int,input().split())
matrix[s][e]= min(matrix[s][e],-t)
# 최소 간선 길이만 저장된 matrix -> edges 에 저장한다.
edges=[]
for i in range(1,n+1):
for j in range(1,n+1):
if matrix[i][j]!=MAX:
edges.append((i,j,matrix[i][j]))
# (시작 노드, 도착 노드, 간선 길이)
2. 벨만 포드를 어떻게 사용할 수 있을까?
단일 노드를 기준으로 시작하는 벨만 포드를 활용하여 어떻게 전체 그래프에서 음의 사이클이 존재하는지 판별할 수 있을까?
아래 사진과 같이 노드 1을 기준으로 벨만 포드를 사용하든, 노드 2를 기준으로 벨만 포드를 사용하든, 음의 사이클이 존재한다는 것을 알 수 있다. 즉, 노드가 서로 연결되어 있는 경우에는 그 중 하나만을 골라서 벨만 포드를 적용해주면 음의 사이클을 판단할 수 있다.
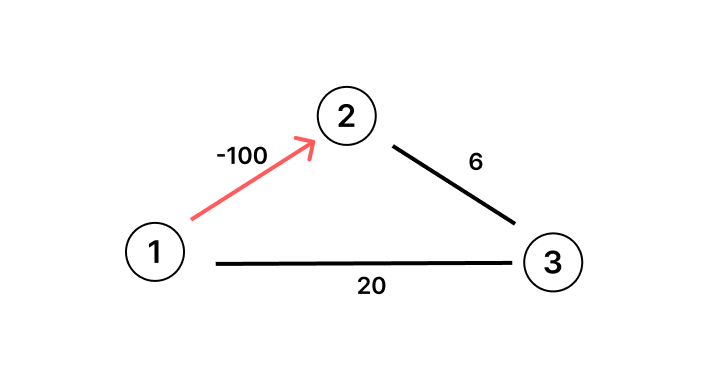
그럼 임의로 1번 노드를 선택해서 벨만 포드를 적용하면 될까? 이렇게 풀 경우 오답이 된다.
아래와 같이 비연결 그래프인 경우, 각 그룹에 대한 사이클을 검사가 필요하다. 특정 노드를 기준으로 사이클 검사를 했을 때, 해당 그룹의 다른 노드는 visited로 방문처리하여 중복 검사를 피하고, 아직 방문하지 않은 노드를 검사하여 각 그룹을 순회하면 된다.

시간 복잡도
초기 인접 행렬을 사용하여 간선을 초기화하였기 때문에 O(V^2) 이 걸리며, 벨만 포드에서 최소 O(VE) 가 걸린다(비연결 그래프인 경우, 각 집합간 노드와 간선의 개수가 줄어들기 때문에 비슷할 것으로 추정). 전체적인 시간복잡도는 O(VE) 이며 시간 내에 동작한다.
코드
import sys
input=sys.stdin.readline
print=sys.stdout.write
INF=int(1e9)
MAX=int(1e4)+1
def bellman_ford(start,n,vidisted,edges):
dist=[INF for _ in range(n+1)]
dist[start]=0
# 해당 노드를 방문처리한다.
vidisted.add(start)
# V-1번 반복하여 dist를 갱신
for _ in range(n-1):
for u,v,w in edges:
if dist[u]==INF:
continue
vidisted.add(u)
vidisted.add(v)
dist[v]=min(dist[v],dist[u]+w)
#음의 사이클 존재 확인
for u,v,w in edges:
if dist[u]!=INF and dist[v]>dist[u]+w:
return True
return False
if __name__=='__main__':
t=int(input())
for _ in range(t):
n,m,w=map(int,input().split())
# 비연결 그래프인 경우가 존재할 수 있으므로, 이를 위해 노드의 방문 여부를 저장한다.
visited=set()
matrix=[[MAX for _ in range(n+1)] for _ in range(n+1)]
# 무방향 그래프이기 때문에, 각각의 방향을 만들어준다.
for _ in range(m):
s,e,t=map(int,input().split())
matrix[s][e]=min(matrix[s][e],t)
matrix[e][s]=min(matrix[e][s],t)
for _ in range(w):
s,e,t=map(int,input().split())
matrix[s][e]= min(matrix[s][e],-t)
## 노드 간 간선의 길이가 최소인 것만 남겨놓고 나머지는 제거
edges=[]
for i in range(1,n+1):
for j in range(1,n+1):
if matrix[i][j]!=MAX:
edges.append((i,j,matrix[i][j]))
# 음의 사이클이 존재한다면, answer= True(음의 간선 존재 O)로 하고 break.
answer=False
for start in range(1,n+1):
if start not in visited and bellman_ford(start,n,visited,edges):
answer=True
break
if answer:
print('YES\n')
else:
print('NO\n')
회고
그래프 내에서 음의 사이클 존재 확인하는 방법
1. 각 그룹 내에서 하나의 노드를 선택하여 벨만포드를 진행
2. 이때, 벨만 포드 함수 내에서 방문처리를 하여 추후 중복 검사를 방지
'문제풀이 > 백준' 카테고리의 다른 글
| 백준 1717 집합의 표현 문제풀이 (0) | 2024.01.20 |
|---|---|
| 백준 1916 최소비용 구하기 문제풀이 (0) | 2024.01.19 |
| 백준 1956 운동 문제풀이 (0) | 2024.01.17 |
| 백준 11657 타임머신 문제풀이 (1) | 2024.01.15 |
| 백준 11404 플로이드 문제풀이 (1) | 2024.01.14 |